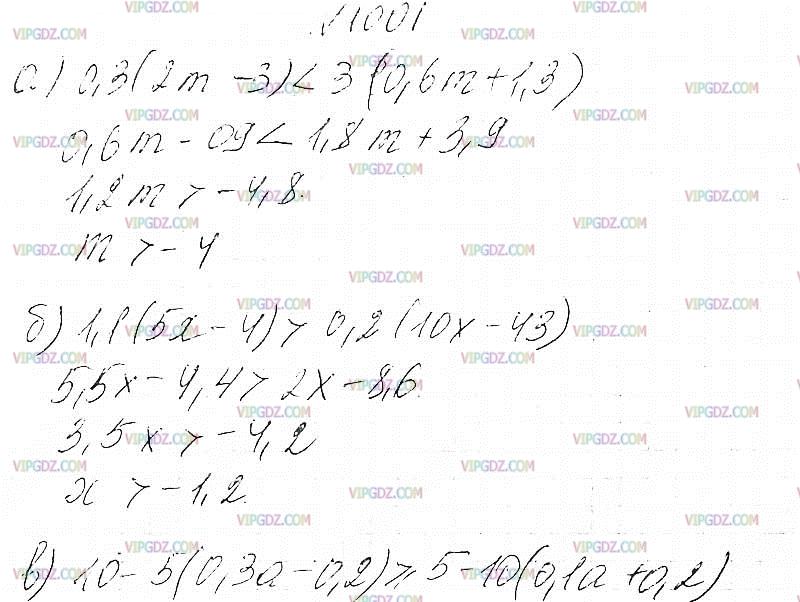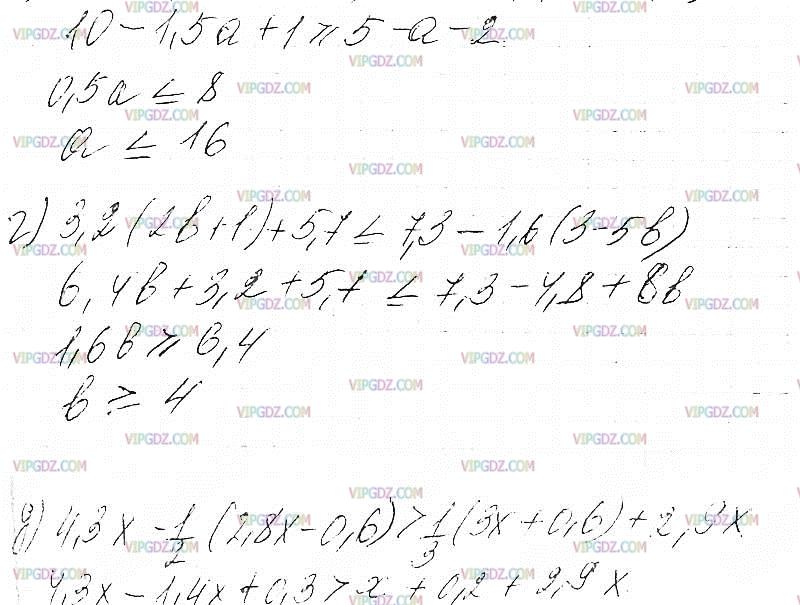Назад к содержанию
Решение на Задание 1001 из ГДЗ по Алгебре за 9 класс: Макарычев Ю.Н.
Решите неравенство:
а) 0,3(2m - 3) < 3(0,6m + 1,3);
б) 1,1(5x - 4) > 0,2(10x - 43);
в) 10 - 5(0,Зa - 0,2) >= 5 - 10(0,1a + 0,2);
г) 3,2(2b + 1) + 5,7 <= 7,3 - 1,6(3 - 5b);
д) 4,3x - 1/2(2,8x - 0,6) > 1/3(3 x + 0,6) + 2,9 x;
е) 2/5(5,5m - 2) - 0,8m < 4,6m - 3/4(3,6m - 1,6);
ж) (2,1y + 2)(0,2y - 3) - (0,7y - 1)(0,6y + 4) >= -83;
з) (1 - 3,6a)(0,2a + 3) + (4 + 0,9a)(0,8a + 10) <= 42,2.
а) 0,3(2m - 3) < 3(0,6m + 1,3);
б) 1,1(5x - 4) > 0,2(10x - 43);
в) 10 - 5(0,Зa - 0,2) >= 5 - 10(0,1a + 0,2);
г) 3,2(2b + 1) + 5,7 <= 7,3 - 1,6(3 - 5b);
д) 4,3x - 1/2(2,8x - 0,6) > 1/3(3 x + 0,6) + 2,9 x;
е) 2/5(5,5m - 2) - 0,8m < 4,6m - 3/4(3,6m - 1,6);
ж) (2,1y + 2)(0,2y - 3) - (0,7y - 1)(0,6y + 4) >= -83;
з) (1 - 3,6a)(0,2a + 3) + (4 + 0,9a)(0,8a + 10) <= 42,2.
Другие задачи из этого учебника
Поиск в решебнике
Популярные решебники
ГДЗ по Алгебре за 9 класс: Макарычев Ю.Н.Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014г.
